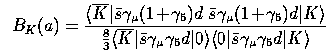Recent Results of Lattice QCD Simulations
The LANL Collaboration 
(This document is also available in
PostScript form.)
Abstract:
We describe recent progress in numerical computations of the
properties of strongly interacting elementary particles.
On the 1024 node Connection Machine-5 (CM-5) at Los Alamos National Laboratory
[ACL],
we are calculating the spectrum of light hadrons, scattering amplitudes
and a variety of electroweak matrix elements.
On the Cray C-90 at
NERSC
we are studying topology and calculating
the kaon B-parameter, BK.
By working on a large lattice (32^4x64), and collecting
a large sample of gauge configurations,
we are able to substantially reduce the
statistical errors compared to previous work.
The level of precision is such that,
combined with existing and future experimental data on weak decays,
these results are beginning to
provide significant tests of the
Standard Model
of particle physics.
Our largest scale computations are on the CM-5.
By coding the computationally intensive
routines in CDPEAC, we attain node speeds of
80-100 MFlops, close to the theoretical maximum.
For the production code, including I/O and communications,
the sustained speed is 25-35 MFlops per node.
Introduction
This document describes the recent results of the LANL collaboration,
a group centered at Los Alamos National Laboratory.
We have been carrying out
large scale simulations of quantum chromodynamics (QCD)
on the 1024 node Connection Machine-5 (CM-5) at the Advanced Computer
Laboratory [ACL] at Los Alamos,
and on the C-90 and other Cray machines at
NERSC.
The former work is as part of the QCD Grand Challenge Applications Group,
a designation shared with the MILC collaboration, whose recent work
is described here by Claude Bernard.
Scientific Objectives
QCD is a theory of quarks (up, down, strange, charm, bottom and top)
interacting with gluons. The gluons bind the quarks into the strongly
interacting particles, the hadrons, that we observe in nature.
The binding is so strong that the quarks and gluons cannot be isolated
as free particles but are observed only as bound states---this
is the phenomenon of "confinement".
The structure of the resulting hadrons is very complicated, and has not
so far been amenable to study using analytic methods.
In particular, low order perturbation theory is not useful, because
the expansion parameter is of order unity.
Non-perturbative techniques are required,
and the only method available is to simulate the theory numerically,
after discretizing space-time into a lattice.
In our calculations, we use lattices of size up to 32^3x64,
i.e. 32 points in the spatial directions and 64 in the (imaginary) time
direction.
There are three major aims of our calculations. First, we wish to
calculate the masses and other properties of the hadrons, in order to compare
them to experimental results and test that QCD is indeed the correct
theory. Because of various approximations that have to be made,
this goal has yet to be attained.
Second, we want to gain insight into the physics behind confinement.
This might open up the possibility of semi-analytic calculations in QCD,
or allow us to understand the behavior of other strongly coupled theories,
such as technicolor or chiral theories.
And, finally, we wish to use lattice methods to allow us to isolate the
effects of QCD which obscure the underlying electroweak
decays of hadrons. This work is the most advanced, and thus we explain
the motivation for it in some detail.
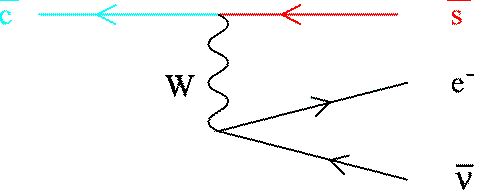
Figure 1: Quark Decay
In addition to feeling the strong force, through interactions with gluons,
the quarks also interact through the weak and electromagnetic interactions,
which form collectively the electroweak interactions.
For example consider a D- meson,
composed of a d quark and an anti-c quark.
This meson decays some of the time through
the quark-level weak interaction process shown in Fig. 1.
c --> s e nu.
The theory of weak interactions predicts the decay rate of the
quarks, up to an overall factor associated with the
c-W-s vertex, |Vcs|**2.
Because the quarks are confined into hadrons, however, the actual decay
is, for example, D-->K0 e nu, where the K0 is a meson
composed of an anti-s quark and a d quark.
An example of the Feynman diagrams contributing to this decay is shown
in Fig. 2.
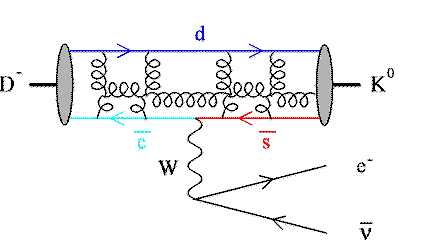
Figure 2: Meson Decay
The binding of the quarks into mesons changes the decay rate,
so that one cannot directly determine |Vcs|**2 from the
experimentally observed rate of the decay process.
In order to make the connection one needs to do a non-perturbative
calculation of the so-called "semi-leptonic form factor",
and it is for this that the lattice is required.
There are many examples of such "electroweak matrix elements" that are
required to extract underlying parameters from existing,
or future, experimental results. Researchers at Fermilab are studying the
mixing and decays of K0 mesons, and the future B-factory at SLAC
will study many decays of the B mesons, which consist of a b-quark
(or anti-quark) and a light anti-quark (or quark).
) Lattice calculations are required to interpret most of the experimental
results. The hope is that we will be able to determine the parameters of the
electroweak interactions (such as |Vcs|**2) in several ways,
and thus test the theory in detail. Any discrepancies would indicated
phenomena beyond the
"Standard Model"
of particle physics (SM).
Resources
For the 1993-4 fiscal year,
we have been allocated 10% of the time on the CM-5 at LANL
(6.1x10^6 node Megabyte hours per quarter),
as part of the Grand Challenge Applications Group grant.
In addition we share, with a group led by A. Soni,
roughly 13000 SU's at NERSC on the C-90 and other Crays.
Results from the CM-5
We proposed that, during the 1993-4 fiscal year, we would
use the time on the CM-5 to generate about 100 lattices of
size 32^3x64 at a coupling beta=6, and do a large
scale analysis on them. This involves calculating quark
propagators at five different masses, and then using these to extract hadron
masses, decay constants, scattering amplitudes and various matrix elements.
We are on target for completing this work, with about 80 lattices
finished at present. In the following
we present some highlights of our results for weak matrix elements.
All results are preliminary.
The coupling constant beta=6 corresponds to a physical lattice
spacing of about a = 0.1 fm, small enough that lattice artifacts
are a relatively small correction to most quantities.
We have previously undertaken exploratory studies at this lattice
spacing on a sample of 35 small (16^3x40) lattices,
the major aim of which was the development of techniques
[1].
In particular, we found that using extended ("smeared") sources we
could significantly improve the signal to noise ratio.
The idea is that mesons and baryons are extended objects, of
typical size 0.5-1.0 fm, and so an operator which can efficiently
create them should be of similar size.
The new calculations are in large part a production run using the methods
we had developed. By working on a lattice having eight times the spatial
volume, we (a) improve the signal, since this is almost equivalent to
an eight-fold increase in statistics,
(b) halve the minimum non-zero spatial momentum, since
Pmin= 2pi/(Ns a), where Ns is the number of spatial points,
and (c) allow the study of smaller quark masses.
The latter improvement is very important since it allows more reliable
extrapolations to the physical up and down quark masses.
An additional improvement is that we are using about three times as many
lattices (100 versus 35), which further decreases the statistical errors.
All our calculations are carried out in the so-called
"quenched" approximation. Mesons and baryons contain, in addition to
the "valence" quarks which determine the quantum numbers of the states,
a complicated cloud of gluons and quark-antiquark pairs. In the quenched
approximation the quark-antiquark component of this cloud is ignored.
This approximation is made in order that the large systems can be studied
with present computer resources: the cost of removing the approximation is
roughly two to four orders of magnitude.
Properties of hadrons that are not particularly dependent on the
quark-antiquark component, for example the masses, decay constants,
and form factors, will not be changed substantially by quenching.
In some cases one can estimate the changes; for the masses they are
in the 10-30% range [2].
Other properties are crucially dependent on the quark-antiquark component,
are will be radically effected by quenching.
Examples are the matrix elements of (F* F) discussed in Ref.
[3].
Our aim in the calculations is to reduce other sources of error---statistics,
finite lattice spacing, finite volume, extrapolation in quark masses---to the
point where quenching is likely to be the dominant error.
Semileptonic form factors
Semileptonic decays of charmed mesons,
such as that illustrated in Fig. 2.
can be directly simulated on present lattices.
The main decays of interest are
- D --> pi e nu
- D --> K e nu
- D --> rho e nu
- D --> K* e nu
These decays are amenable to lattice calculations as they only
involve a single strongly interacting particle in both initial and final
states. The unknown part of the decay amplitude is a matrix element such as
<K*(p') | J(q) | D(p)>
q=p-p' is the four-momentum carried by the weak current J and
is the sum of the momenta of the e and nu in the actual decay.
If we could calculate these matrix elements from first principles, for
the physical range of q, then we could predict all aspects of the decay
process in terms of a single unknown constant, the appropriate weak
coupling constant for the underlying quark decay.
This element is Vcd for D-->(rho or pi)
e nu and Vcs for D-->K(*) e nu.
In fact, within the standard model, if there are only
three generations, we can use other results to
predict Vcd and Vcs to good accuracy.
The lattice calculations thus allow a test of the consistency of the SM.
In addition, experiments have not yet fully measured all aspects of the
angular distribution of the decays, allowing the opportunity
for lattice calculations to predict these distributions.
In practice, lattice calculations cannot access the full physical range of
q.
Instead they work in a small range of q^2 around zero,
and assume pole-dominance to extrapolate to larger q^2.
This restriction arises because the lattice results have small errors only
for small spatial momenta.
In our calculations we set p=0, while
q/(2pi/Ns) = (0,0,0), (1,0,0), (1,1,0), (1,1,1) and (2,0,0),
where Ns is the number of spatial lattice points.
Using a larger Ns decreases the step size in q, and thus increases
the number of usable momenta.
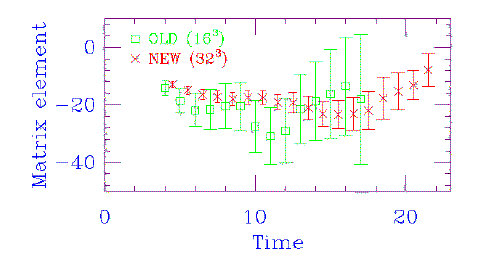
Figure 3: Form factor data
To give an indication of the improvement in quality of the results that
we have achieved with our new simulations, we compare to our old data
on 16^3x40 lattices in Fig. 3.
In the plot, the lattice kaon is created at t=0, propagates to the
Euclidean time t, where it is converted by the weak current
J into a D-meson, which propagates to time t=25
(31) for the new (old) data.
We have divided by two-point correlators in such a way that the signal
should have constant magnitude.
The matrix element is for the spatial
part of the vector current, J = Vi, inserting
momentum q=(2pi/16,0,0).
We have adjusted the overall scales so that the size of the errors can
be directly compared, and we see that there has been both a substantial
reduction in the errors, and a lengthening of the "plateau" region.
We have done a preliminary analysis of 50 of the new lattices.
We find, for example, that for D --> K e nu the form factor is
f+(q^2 = 0) = 0.81 +- 0.03 +- 0.03
The first error is statistical, the second the systematic
error due to extrapolation to the physical light quark masses.
This form factor governs the rate for D --> K e nu decay.
The experimental result for this decay, together with the
value of |Vcs| required for consistency of the three generation SM,
implies f+(0) = 0.77 +- 0.04 [4].
Typical previous lattice results are
0.65 +- 0.18 [5]
and 0.90 +- .08 +- 0.21 [6].
We see that that the errors have been substantially reduced,
and are now at the point where discrepancies with the SM could appear.
The most likely source of any such discrepancy is our use of the
quenched approximation.
Turning this around, we can see that, for this quantity,
the quenched approximation is apparently reliable to about 10%.
Assuming this accuracy applies to other form factors, we can make predictions.
In particular, in the decay D --> K* e nu, we find
A2(0)/A1(0) = 0.93 +- 0.27 +- 0.09.
This should compared to the previous results 0.7 +- 0.4 [5]
and 0.70 +- 0.16 (+0.20-0.15} [6]
One early experiment found a ratio consistent with zero (with large errors),
whereas the latest result is 0.82 +- 0.23 +- 0.11.
Results from NERSC
We have used the Cray-2's and the C-90 extensively for the last several
years. While slower than the CM-5, these machines have the advantages
of stability, user-friendliness, and large storage capacity. We have collected
a large database of lattices and quark propagators using which we have
repeated calculations with refined methods, and tested new techniques.
The kaon B-parameter BK
The most significant result to emerge from our work at NERSC is that for
the kaon B-parameter
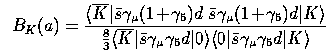
Knowledge of this quantity is essential to extract a value for Vtd
(the coupling of the W-boson to the t and d quarks)
from the experimentally measured CP-violating part of the
Kbar-K mixing amplitude, and the lattice offers the only first
principles method of calculation.
We have gradually learned to control the systematic errors
in the calculation of BK, using a combination of theoretical analysis
and numerical improvements. Our result for the scale invariant B-parameter
is [7]
BK = 0.825 +- 0.027 (stat) +- 0.025 (syst.)
The systematic error does not include that due to quenching, or
our use of degenerate quarks, but there is evidence that the additional
errors are not larger than the quoted errors.
BK is thus one of the most reliably determined lattice quantities,
and, furthermore, the lattice determination is more accurate than those using
other methods. This result is now being used in analyses of the constraints on
the consistency of the standard model.
Topology
In our most recent work at NERSC we have been studying the
topological charge and the distribution
of charge density on our gauge configurations.
Our overall aim is to gain insight into the role of instantons in the
physics of confinement, and in particular to make detailed comparisons
with the instanton liquid model of Shuryak.
Previous studies have used various definitions of the density,
and we have undertaken a careful comparison of these methods,
paying particular attention to numerical difficulties [8]
Computational issues
The most computationally challenging part of our work is that on the CM-5.
Lattice QCD is naturally parallel, since the same operations
must be performed at each space-time point.
These operations involve exchanging information with adjacent
sites on the hypertorus, and performing computations at each site
(e.g. 3x3 complex matrix multiplies).
Our basic code is written in CM-Fortran (CMF), including the
communication, which is done using the command CSHIFT.
To use the machine efficiently, we have found it necessary
to write the computationally intensive on-node routines
in the C-like assembly language CDPEAC.
With the present compiler this gives speed ups of 1.5-3.
This arrangement also makes our code quickly adaptable to new versions of
the Connection Machine, since the small modules can be developed quickly
for a new processor.
Our CDPEAC codes sustain node speeds of between 80 and 100 MFlops,
the latter being close to the theoretical maximum,
as long as the particular computation allows
chaining of adds and multiplies.
The overall speed of our codes is significantly slower,
mainly because of necessary internode communication.
Our gauge update code sustains 25 MFlops/node. For a 32^3x64 lattice
it requires 3 GigaBytes of memory, and thus
runs on partitions of 256 nodes or larger. On a 256 node partition
it takes 9 hours to generate an independent lattice
(2000 overrelaxed and 400 Metropolis sweeps).
Our propagator code for Wilson fermions requires 6 GigaBytes of memory,
and sustains a node speed of 35 MFlops on a 256 node partition.
It takes 16 hours to calculate propagators at 5 different masses with
and without a meson source.
Finally, we need to combine the propagators into the various meson correlators
we use to extract masses, form factors, etc. This code spends roughly
60% of its time doing i/o from the 25 GigaBytes of
data (lattices and propagators) stored on the scalable disk array.
It requires the equivalent of 16 hours on a 256 node partition,
although in practice we use five separate runs,
two of which require a 512 node partition.
We save the configurations and the three light quark propagators on
exabyte tapes, so that as we develop further analysis ideas we can test
them out with relatively small cost in computer time.
Our code is very demanding of the CM-5. On various occasions it has
found problems which the standard diagnostics did not uncover.
In a recent example, the machine was reporting single bit memory errors,
which should have been corrected in hardware, but which were causing our
code to crash unreproducibly. This suggested an intermittent hardware problem.
Further investigation by Thinking Machines Corporation led to the
discovery of memory errors related to fluctuations in voltage and temperature.
An overhaul of the entire CM-5 will be undertaken in July 1994 to correct
this problem.
Parts of our code are now used as diagnostics by TMC.
Future Plans
In the remainder of this fiscal year, we intend to complete
the analysis on our proposed sample of 100 lattices at beta=6.0.
We have only mentioned the highlights above---we are calculating a large
number of quantities, and in all almost all cases have better statistical
control than that of previous calculations.
We propose to extend this work in fiscal year 1994-5 in several ways:
-
Reduce lattice spacing errors either by using a smaller lattice spacing
or an improved action.
-
Include non-relativistic quarks so as to directly study B mesons.
-
Implement staggered fermions.
References
- D.
Daniel, R. Gupta, G. Kilcup, A. Patel and S. Sharpe,
"Phenomenology with Wilson fermions using smeared sources"
Phys Rev D46 (1992) 3130.
[Abstract]
R. Gupta, A. Patel and S. Sharpe,
"The pi-pi scattering length with Wilson fermions"
Phys Rev D48 (1993) 388.
[Abstract]
G. Kilcup, S. Sharpe, R. Gupta and A. Patel,
"Lattice Calculation of the Kaon B Parameter"
Phys Rev Lett 64 (1990) 25.
- J. Labrenz and S. Sharpe,
"Quenched chiral perturbation theory for baryons"
Nucl Phys B (Proc. Suppl.) 34 (1994) 335.
[Abstract]
- R. Gupta and J. Mandula,
"Matrix Elements of the Singlet Axial Current in the Proton"
LA-UR-94-440, Feb 1994.
[Abstract]
- M. Witherell, Talk at Int. Symp. on
Lepton and Photon Interactions at High Energies, Cornell University, 1993,
UCSB-HEP 93-06.
- A. Abada et al., Nucl Phys B416 (1994) 675.
[Abstract]
- C. Bernard, A. El-Khadra and A. Soni,
Phys Rev D43 (1992) 2140, Phys Rev D45 (1992) 869.
- S. Sharpe, Nucl Phys B (Proc. Suppl.) 34 (1994) 403.
[Abstract]
- J. Grandy and R. Gupta,
Nucl Phys B (Proc. Suppl.) 34 (1994) 164.
[Abstract]
Created by: kilcup@osu.edu [15 July 94]